 Imagine this scenario: A murder case that went cold 20 years ago is reopened thanks to newly available DNA-based forensics. The state, lets say Arizona, has a large database of DNA. This isn’t the DNA deposited from newborns that David discussed a few weeks ago, but DNA from convicted criminals and really anyone who’s been brought up on charges in the last few years, whether or not they were eventually found innocent. DNA from a piece of evidence in that 20-tear-old case matches DNA in the database, the suspect is brought in a questioned. He has no alibi for what he was doing on day X 20 years ago. Charges are filed, a jury is called, and the suspect is convicted on the strength of a DNA match. Justice is served, right? Maybe, but maybe not.
Imagine this scenario: A murder case that went cold 20 years ago is reopened thanks to newly available DNA-based forensics. The state, lets say Arizona, has a large database of DNA. This isn’t the DNA deposited from newborns that David discussed a few weeks ago, but DNA from convicted criminals and really anyone who’s been brought up on charges in the last few years, whether or not they were eventually found innocent. DNA from a piece of evidence in that 20-tear-old case matches DNA in the database, the suspect is brought in a questioned. He has no alibi for what he was doing on day X 20 years ago. Charges are filed, a jury is called, and the suspect is convicted on the strength of a DNA match. Justice is served, right? Maybe, but maybe not.
So here’s the funny bit. The problem with this scenario has nothing to do with genetics, forensic science, or data storage and access. It’s really not even about crime and justice. It’s about your birthday.
Introduction to Statistics teachers love to begin the first day of class with a demonstration of the birthday paradox. Take any given class of 23 or more students and have them begin calling out their birthday (month an day, although the day month format is also appropriate). Odds are better than 50% that two students will share the same birthday, and everyone will be amazed. What an incredible coincidence! Not really.
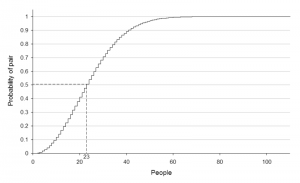
Here’s what’s happening: For any given student in a class of 23, the odds that one person in the class will share their birthday with a specific student is 1/365, but the odds of sharing a birthday with any student in the class is 22/365. Now call on the next student. Their odds of sharing a birthday with someone else are 21/365 (we already established that student number 1 shares no birthday). For the student after that, the odds go down to 20/365, and so on down the line. So the odds that any student shares a birthday with any other student in the class is roughly (number of students -1)!/365. The actual equation is a little more complicated than that, but conceptually the same. At 23 students the odds are better than 50%, around 50 students the odds are closer to 99%.
This is a problem inherent in randomly sampling from a large database. The odds of any two students sharing the same birthday is low, but by drawing from a large enough pool of students, you guarantee a match.
Let’s say you have twins in the class. You know you have twins, but you don’t know who they are. Assume their fraternal and look nothing alike, but share the same birthday. Let’s also assume there are 100 students total, enough to ensure that there will be a random birthday match. If you were to decide to find these twins by calling out birthdays, there’s be no guarantee that the match would be the twins you were looking for. Assume you know one of the twins, even then, the odds of a random match in a class of 100 would be a little more than 25%. A test that’s only right 3/4 of the time is not very good.
But assume you can do a little investigation before hand. You look at your students last names, the states they’re from, how they interact which each other. You take all that evidence and use it to decide who your likely twins will be. Then you test their birthdays. Because you’re not drawing from a random pool, the odds that non-twins who happen to have the same last name, state of origin, and treat each other like siblings will also share the same birthday is astronomically low. So low that you can confidently claim that these two students are definitely twins.
What if instead of secret twins in a class, we’re talking about DNA at a crime scene. And instead of a few hundred students, we’re talking about millions of people’s archived DNA. The chance of mismatch is much lower than 1/365, but the sample size is much higher, and the consequences of such a mismatch are dire. Querying DNA from a crime scene against a database ensures that some small fraction of the time there will be a false positive, and an innocent person will be arrested, possibly tried, and possibly convicted, especially with cold cases where DNA is the only remaining evidence.
So how should the justice system use DNA evidence? The same way they use regular evidence. If you have DNA at the crime scene, establish a likely suspect first, then test their DNA for a match. This will reduce the possibility of false positives to near zero. But a suspect generated by querying a DNA database first may just be unlucky.
Several sources have tackled this issue in the past few years. The state of Texas was recently caught storing DNA data from newborns illegally. Who has the right to your genetic information is going to be a huge debate over the next decade. Ready access to genetic information is going to be a cornerstone of both our social and legal systems and the dialogue needs to remain engaged. But it’s important to remember that this problem is not the result of emerging technologies, but one of simple statistics.
~Southern Fried Scientist
Are there any confirmed cases of a DNA database search implicating the wrong person?
How does the DNA database implicate the wrong person? What kind of tests do they run to match DNA samples? Wouldn’t the problem be solved by comparing more and more of the genome for matching (ideally, the whole damn thing)?
Currently forensics test 13 microsatellite loci. Whole genome sequencing would be exorbitantly expensive, especially when the solution is already out there – require probable cause to search someone’s genome, just like if it were their car or home.
http://articles.latimes.com/2008/jul/20/local/me-dna20
Not in court (that we know of), but in the practice of doing DNA investigations
Well, it’s expensive now. Just attended a lecture from a company that has it down to $1000/person using microarray tech, and it can be done in a matter of a day or two. Give it 20 years and I bet it’ll be pretty cheap to sequence whole genomes. Just sayin’.
20 years is an awfully long time to be sitting in jail if you get convicted on DNA evidence alone today. Especially since the problem is not in the data, but in the way the data is queried.
A few years ago there was an hilarious snafu when a Scottish police officer just happened to have near identical fingerprints to those found on the crime scene, completely by chance (they caught the perp and confirmed it).
Sequencing the genome doesn’t matter. The current technique works fine, as long as you don’t sample from a random pool.
Assume you know one of the twins, even then, the odds of a random match in a class of 100 would be a little more than 25%. A test that’s only right 3/4 of the time is not very good.
Is this correct? I think my logic is not following your logic.
I know the actual statistics are a little more complicated and I’m guilty of oversimplifying, but the odds would be pretty close to 99/365. You have 99 students, each has a chance of 1/365 (assuming even distribution of birthdays) to match the twin.
The Wikipedia entry on the Birthday Paradox has a much better summary of how it works.
If it were a matter of guilty/ non-guilty, life/ no life in prison, don’t you believe the “exorbitantly expensive” dues would be justified (no pun intended) by the reassurance that a legally sound conviction took place?
Further, “Sequencing the genome doesn’t matter. The current technique works fine, as long as you don’t sample from a random pool.”
How does the current technique “work fine” if the basis of this article exemplifies how flawed this system truly is?
I think you missed a bit of the point. The problem isn’t with the technology. If you compare DNA from a crime scene to DNA from a suspect and find a match at 13 loci, you’ll have as much confidence in the result as if you used a full genome. The problem is that when you use DNA to find a suspect by querying a database, you increase the chance of a false match. This problem exists regardless of the whether you use DNA, fingerprints, dental records, biometrics, or any identifier that has a sufficiently large database.
The problem is how we use and misuse the data.
So, I understand your issues with the DNA database, however, the information that is used for reports is only as relevant and important as the analyst reporting them out. There are a number of EXCELLENT reasons to have the database and the people that have a problem with it are usually the ones that have not been affected by a violent episode. Imagine being able to connect a deceased, missing person with their loved ones in another state, it happens. Using rare occurring scenarios is not a reason to not have the database. Yes the occasional weak match can happen, but, there are rules in place to make sure the analyst is using discretion in results. There are so many benefits to having the database available, like linking a solved case to an unsolved case (just one example). Again, the people that have the biggest problem with the database have rarely been affected by a tragedy that is unsolved.
So it’s ok to mine people’s personal information without probable cause? It’ll also be easier to catch criminals if police could just enter anyone’s house at any time without a warrant.